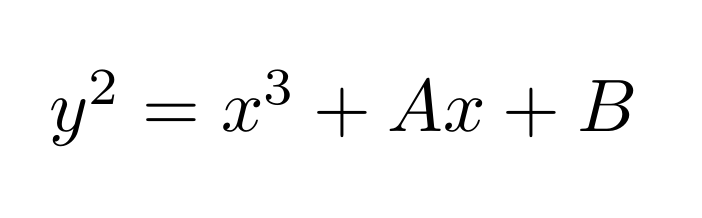Division Algebra Over Algebraically Closed Field

16 Mar, 2021

Division algebras can be classified in terms of fields. Every 4-dimensional central simple algebra over a field F is isomorphic to a quaternion algebra.

Distributive Property Definition Uses Examples

In fact it is either a two-by-two matrix algebra or a division algebra.

Division algebra over algebraically closed field. Remember that extension-fields are just a special case of division algebras. The fact that every finite dimensional division algebra is trivial is not only true over an algebraically closed field but it is in fact equivalent to the field being algebraically closed. Division algebras can be classified in terms of fields.

Let KF be any field extension. Take a Banach space and the linear endomorphisms under composition then that is a unital associative -algebra with complete norm thus a Banach algebra. If D is a central division algebra over K for which the index has prime factorisation.

Over any algebraically closed field such as there are no finite dimensional associative division algebras except itself. There are infinite dimensional associative algebras. A field F is called algebraically closed if every nonzero polynomial px a 0 x n a 1 x n-1 a n x 0 a i F a 0 0 n 0 has a root r F.

A field F is called algebraically closed if every nonzero polynomial p x a0xn a1xn-1 anx0 ai F a0 0 n 0 has a root r F. If every polynomial over F of prime degree has a root in F then every non-constant polynomial has a root in F. Let a D.

1 It follows that a field is algebraically closed if and only if every polynomial over F of prime degree has a root in F. The algebraic closure of F in K is the subset of K consisting of elements algebraic over F. Does not have any rational or real solution.

We claim that if D is a finite-dimensional division algebra over an algebraically closed field k then in fact D k. Let KF be any field extension. As proof if x D then consider the inverse closed subring of D generated by k and x.

Let k be an uncountable algebraically closed field and let A be a countably generated left Noetherian k-algebra. Here is the statement and then the proof. If S is a simple subalgebra of a central simple algebra A then dim F S divides dim F A.

A field containing F is called an algebraic closure of F if it is algebraic over F roughly speaking not too big compared to F and is algebraically closed big enough to contain solutions of all polynomial equations. Suppose we have a division algebra D over an algebraically closed field F of finite dimension n. We conclude that all subfields of the quotient division algebra of a countably generated left Noetherian domain over k are finitely generated extensions of k.

The endomorphism ring of any simple R -module is a division ring. The algebraic closure of F in K is a field and is algebraically closed in K. On the other hand a finite dimensional division algebra over an algebraically closed field k must be equal to k this is because any element generates a finite dimensional subfield over k which must be equal to k.

Thus an algebra is an algebraic structure consisting of a set together with operations of multiplication and addition and scalar multiplication by elements of a field and satisfying the axioms implied by vector space and bilinear. Suppose we have a division algebra D over an algebraically closed field F of. This is a finite hence algebraic extension of k hence must be equal to k.

The subfield F of K is said to be algebraically closed in K if it is its own algebraic closure in K. The multiplication operation in. Thus if it would be true over pseudo-algebraically closed fields we would have that a field is algebraically closed if.

In mathematics an algebra over a field is a vector space equipped with a bilinear product. The rational and the real numbers are not algebraically closed since the equation x 2 1 0. Mutative division algebra is the same as that in the commutative case ie over a eld if you remember to distinguish between left and right modules since.

On the other hand Bell has shown 5 that this condition is automatically satisfied for a countably generated right noetherian algebra over an uncountable algebraically closed field These. Then we show that A k K is left Noetherian for any field extension K of k.

Https Www Ias Ac In Public Volumes Reso 004 08 0036 0057 Pdf

Algebraically Closed Field In A Division Ring Mathematics Stack Exchange

Interactive Digital Math Activities Math Activities Google Math Activities Google Drive Math

Part D Working With Algebraic Structures 60 Minutes Annenberg Learner

Http Math Mit Edu Classes 18 785 2015fa Lecturenotes4 Pdf

Series And Parallel Circuit Lab Series And Parallel Circuits Circuit Science Lessons Elementary

Http Math Bu Edu People Jsweinst Teaching Ma542spring20 April27 Pdf

Http Math Ucsd Edu Nwallach Appendixa Pdf

Ccss Lesson Matching Algebraic Expressions To Words To Areas Of Shapes Algebraic Expressions Education Math Middle School Math

The Algebraic Expressions Have The Variables And The Constants The Algebraic Expressions Are The Finite Algebraic Expressions Like Terms Expression Definition