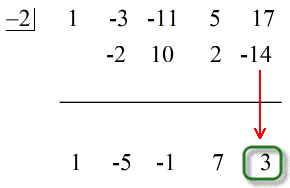Synthetic Division Remainder Not Zero

06 Aug, 2021

To set up the problem first set the denominator equal to zero to find the number to put in the division box. Multiply the entry in the left part of the table by the last entry in the result row under the horizontal line.

Remainder Theorem Definition Examples Video Lesson Transcript Study Com

The remainder is not zero.

Synthetic division remainder not zero. Synthetic Division Answers. To set up the problem we need to set the denominator zero to find the number to put in the division box. 1 2 1 5.

X6 5 x5 5 x4 5 x3 2 x2 10 x 8 0. In the context of the Remainder Theorem this means that my remainder when dividing by x 2 must be zero. Drop the first coefficient below the horizontal line.

N -a 1 n -1 0 then they will be in the set p q where p factors of the constant a 0. 1 The remainder is 3. Set up the synthetic division to solve as shown below.

C 2. If the remainder is zero then x 1 is a zero of x 3 1. Following are the steps required for Synthetic Division of a Polynomial.

Setting this equal to zero I get that x 2 is the other zero of the quadratic. Multiply that number you drop by the number in the box. Then the numerator is written in descending order and if any terms are missing we need to use a zero.

Drop down the first term then multiply and add to the next term. Using this information Ill do the synthetic division with x 4 as the test zero on the left. Learn how to perform synthetic division on polynomialsFor more help visit my website.

This college algebra and precalculus video tutorial explains how to use synthetic division to divide polynomials evaluate functions using the remainder theo. If the remainder is not zero discard the candidate. If the remainder is 0 the candidate is a zero.

Use the Remainder Theorem to determine whether x 4 is a solution of. Repeat step two using the quotient found with synthetic division. If there are rational zeros in the polynomial.

I divided by a negative and the signs on the bottom row alternated plus minus plus minus. C - 2 c 2 inside the box. Next make sure the numerator is written in descending order and if any terms are missing you must use a zero to fill in the missing term finally list only the coefficient in the division problem.

Then x 2 is not a zero of f x. To do the initial set-up note that I needed to leave gaps for the powers of x that are not included in the polynomial. Note that you can use long division instead of synthetic division but its almost always faster and easier to use synthetic division.

Because the remainder is zero this means that x 3 is a factor and x 3 is a zero. For x 4 to be a factor you must have x 4 as a zero. As you can see the remainder is non-zero so x 6 is not a solution of 2 x3 7 x2 16 x 6 0.

Use the result to find all zeros of f. X 3 2x 2 x 5 x 2 The opposite of the constant in our binomial is 2. So if the remainder comes out to be 0 when you apply synthetic division then x - c is a factor of f x.

All Even Exponents take this shape on a graph. In the synthetic division I divided by x 3 and arrived at the same result of x 2 with a remainder of zero. 2 1 2 1 5 2 0 2.

But Id like you to notice something else. Use synthetic division to evaluate a given possible zero by synthetically dividing the candidate into the polynomial. Add the obtained result to the next coefficient of the dividend and write down the sum.

5 1 5 7 34 1 5 5 0 0 1 0 7 0 7. Yes x 4 is a factor of 2 x5 6 x4 10 x3 6 x2 9 x 4. Also because of the zero remainder x 2 is the remaining factor after division.

Finally construct a horizontal line just below the coefficients of the dividend. If the remainder is zero it is a root take the numbers from below and assemble the polynomial in order of x X2. To learn about Long Division of Polynomials Remainder and Factor Theorems Synthetic Division Rational Zeros Theorem.

The Remainder Theorem states that f c the remainder. Set up the synthetic division and check to see if the remainder is zero. Beginmatrixbeginarrayr -2 endarray underline begin.

Px -x5-5x3-x22 qx x2 The synthetic division table is. Use synthetic division to divide by x - 2. Whatever its product place it above the.

Fx a x a n xn. Therefore if you find a remainder of zero after performing synthetic division the number listed out front referred to as an in the definition above evaluates to zero or f a 0. Our coefficients and constant are.

That is I followed the practice used with long division and wrote the polynomial as x 3 0x 2 0x 1 for the purposes of doing the division. If you forget to leave gaps your division. Look at the signs on the numbers in the bottom row.

Since the remainder is zero then x 4 is indeed a zero of 2 x5 6 x4 10 x3 6 x2 9 x 4 so. If not zero it is not a root.

Synthetic Division Chilimath

Use Synthetic Division To Find The Quotient Q And Remainder R When Dividing The Polynomial 2x2 X By X 1 How Do I Solve This Quora

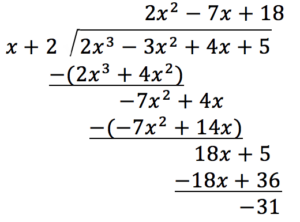
Synthetic Division College Algebra

Here S A Freebie For Your Algebra 2 Honors Students Practice In Groups Or Use As A Take Home A Algebra Activities High School Polynomials High School Algebra